Question

What is the axis of symmetry for f(x) = −2x2 + 20x − 42?

Answer 1

The axis of symmetry is the vertex's x value.. You can find this by using the following formula:

`(-b)/(2a)`

`(-20)/(2(-2)) = (-20)/(-4) = 5`

So x = 5 which mean our axis of symmetry is at x = 5

Answer 2

The axis of symmetry is x=5

Explanation:

Given function is :

f(x)=
`2x^(2) +20x-42`

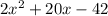
We can use the formula
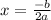`x= (-b)/(2a)` for the axis of symmetry.

`(-20)/(2(-2)) =5`

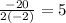
Therefore, the axis of symmetry is x=5

Axis of symmetry is the line of symmetry of a parabola that divides it into two equal halves. These halves are reflections of each other about the line of symmetry.