We can see from points
(2,1) means for n = 2, a = 1
(3,3) means for n = 3, a = 3
(4,9) means for n = 4 , a= 9
Now try to see relation in outputs 1,3,9.
We can write 1 as

3 as
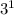
9 as

So (2,2) would mean for n =2, a = 1 or
 ----------------(1)
----------------(1)
(3,3) would mean for n = 3, a = 3 or
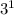 -------------(2)
-------------(2)
(4,9) would mean for n = 4, a = 9 or
 --------------------(3)
--------------------(3)
From (1) we can see for n =2, exponent on 3 is 0
From (2) we can see for n =3, exponent on 3 is 1
From (3) we can see for n =4, exponent on 3 is 2
So we can see the pattern whatever is n value its 2 less is the exponent on 3. So for n exponent on 3 will be n-2
For n = n, a =

Now looking at options given
option (A)
 doesnt match to
doesnt match to

so its incorrect
------------------------------------------------------------------------------------------------------
option (B)
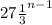 doesnt match to
doesnt match to

so its incorrect
----------------------------------------------------------------------------------------------------------
option (B)
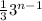 which we can also write as
which we can also write as
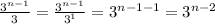
we subtract exponents when dividing same bases so we subtracted exponent 1 from n-1 and finally got

so option (c) matches and is right answer
---------------------------------------------------------------------------------
option (D)
 doesnt match to
doesnt match to

so its incorrect