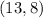Question

Parallelogram FGHI on the coordinate plane below represents the drawing of a horse trail through a local park:

Quadrilateral FGHI is shown on the coordinate plane with coordinates F at −6, −1; G at −1, −1; H at −2, −4; and I −7, −4. Point A is at 3, 8 and point D is at 1, 2.

In order to build a scale model of the trail, the drawing is enlarged as parallelogram ABCD on the coordinate plane. If two corners of the trail are at point A (3, 8) and point D (1, 2), what is another point that could represent point B?

(10, 8)
(13, 8)
(8, 8)
(6, 8)

Answer 1

13,8

Explanation:

just took the test

Answer 2

we know that

Parallelogram is a quadrilateral with opposite sides parallel and equal in length

so

`FI=GH\\FG=IH`

`AD=BC\\AB=DC`

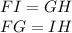
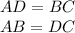
we have

`F(-6,-1) \\G(-1,-1)\\H(-2,-4)\\I(-7,-4)\\A(3,8)\\D(1,2)`

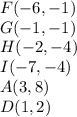
Step 1

Find the distance FI

we know that

the distance between two points is equal to the formula

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

`F(-6,-1) \\I(-7,-4)`

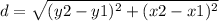
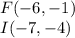
substitute the values

`d=\sqrt{(-4+1)^(2)+(-7+6)^(2)}`

`d=\sqrt{(-3)^(2)+(-1)^(2)}`

`dFI=√(10)\ units`

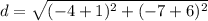
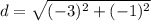
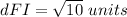
Step 2

Find the distance FG

we know that

the distance between two points is equal to the formula

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

`F(-6,-1) \\G(-1,-1)`

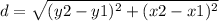
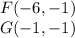
substitute the values

`d=\sqrt{(-1+1)^(2)+(-1+6)^(2)}`

`d=\sqrt{(0)^(2)+(5)^(2)}`

`dFG=5\ units`

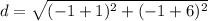
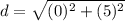
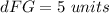
Step 3

Find the distance AD

we know that

the distance between two points is equal to the formula

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

`A(3,8)\\D(1,2)`

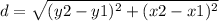
substitute the values

`d=\sqrt{(2-8)^(2)+(1-3)^(2)}`

`d=\sqrt{(-6)^(2)+(-2)^(2)}`

`dAD=√(40)\ units`

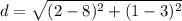
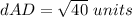
Step 4

Find the scale factor

we know that

the scale factor is equal to

`scale\ factor=(dAD)/(dFI)`

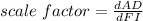
we have

`dFI=√(10)\ units`

`dAD=√(40)\ units`

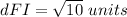
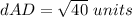
substitute the values

`scale\ factor=(√(40))/(√(10))=2`

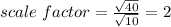
Step 5

Find the coordinate of point B

we know that

the length side of the segment AB is equal to

`dAB=scale\ factor*dFG`

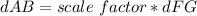
we have

`scale\ factor=2`

`dFG=5\ units`

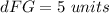
substitutes

`dAB=2*5=10\ units`

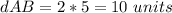
the x-coordinate of point B is equal to the x-coordinate of point A plus the distance AB

`Bx=Ax+dAB`

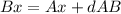
where

Bx------> is the x-coordinate of point B

Ax-------> is the x-coordinate of point A

dAB------> distance AB

susbtitute

`Bx=3+10=13`

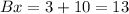
the y-coordinate of point B is equal to the y-coordinate of point A

`By=8`

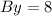
therefore

the coordinate of point B is
`(13,8)`

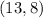
the answer is the option

`(13,8)`