Question

Simplify y to the 1/3 ÷ y to the -3/2 y to the 1/2

Answer 1

`(y^(1)/(3))/(y^(-3)/(2)y^(1)/(2))`

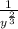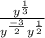
The rule of exponent says , when two terms with same base are in multiplication , the exponents gets added.

for example

a^m * a^ n = a^(m+n)

and when two terms are in division with same base , the exponents are subtracted

for example

a^m /a^n = a^(m-n)

So applying these rules

we get

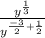
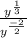
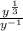
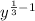
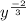
`\frac{y^(1)/(3)}{y^{(-3)/(2)+(1)/(2)} }`

=
`\frac{y^(1)/(3)}{y^{(-2)/(2)}}`

=
`(y^(1)/(3))/(y^(-1))`

=
`y^{(1)/(3)-1}`

=
`y^(-2)/(3)`

=
`\frac{1}{y^{(2)/(3)}}`