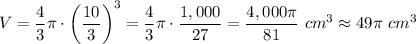Question

Find the volume of the sphere in terms of
`\pi`

Answer 1

check the picture below.

so we use the blue triangle to get the slanted length of the isosceles triangle, that means the upper-tangents are each 13 - 5, as you see there, then we use the yellow triangle with those lengths, and the pythagorean theorem to get r.

`image`

Answer 2

Look at the picture.

Use the Pythagorean theorem to calculate the length of a side x:

`x^2=5^2+12^2\\\\x^2=25+144\\\\x^2=169\to x=√(169)\to x=13\ cm`

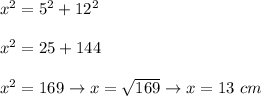
Use the formula of a radius of a circle inscribed in a triangle:

`r=(2A_\Delta)/(a+b+c)`

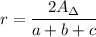
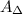`A_\Delta` - an area of a triangle

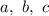`a,\ b,\ c` - the sides of the triangle

Calculate:

`A_\Delta=(10\cdot12)/(2)=60\ cm^2`

`r=(2\cdot60)/(13+13+10)=(120)/(36)=(10)/(3)\ cm`

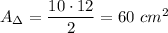
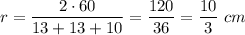
The fromula of the volume of a sphere:

`V=(4)/(3)\pi r^3`

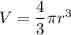
Substitute:

`V=(4)/(3)\pi\cdot\left((10)/(3)\right)^3=(4)/(3)\pi\cdot(1,000)/(27)=(4,000\pi)/(81)\ cm^3\approx49\pi\ cm^3`