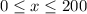General Idea:
Domain of a function means the values of x which will give a DEFINED output for the function.
Applying the concept:
Given that the x represent the time in seconds, f(x) represent the height of food packet.
Time cannot be a negative value, so
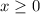
The height of the food packet cannot be a negative value, so
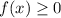
We need to replace
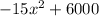 for f(x) in the above inequality to find the domain.
for f(x) in the above inequality to find the domain.
![-15x^2+6000\geq 0 \; \; [Divide \; by\; -15\; on\; both\; sides]\\ \\ (-15x^2)/(-15) +(6000)/(-15) \leq (0)/(-15) \\ \\ x^2-400\leq 0\;[Factoring\;on\;left\;side]\\ \\ (x+200)(x-200)\leq 0](https://img.qammunity.org/2019/formulas/mathematics/high-school/f7mf5job3zx63szj48h7i13f5fbmw32j3t.png)
The possible solutions of the above inequality are given by the intervals
![(-\infty , -2], [-2,2], [2,\infty )](https://img.qammunity.org/2019/formulas/mathematics/high-school/7w3qou4b340qin8zek2vcrqd6dq2zgnyy4.png) . We need to pick test point from each possible solution interval and check whether that test point make the inequality
. We need to pick test point from each possible solution interval and check whether that test point make the inequality
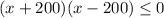 true. Only the test point from the solution interval [-200, 200] make the inequality true.
true. Only the test point from the solution interval [-200, 200] make the inequality true.
The values of x which will make the above inequality TRUE is
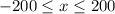
But we already know x should be positive, because time cannot be negative.
Conclusion:
Domain of the given function is