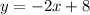Question

What is the slope-intercept equation of this line? (0,8) (6,-4)

Answer 1

Slope-intercept form follows the format:
`y=mx+b`

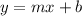
where m is the slope, b is the y-intercept, and x and y is a given point found on the line.

To find the slope given two points, we use the equation:

`(y_(2)-y_(1))/(x_(2)-x_(1))`

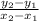
where subscripts 1 and 2 correspond to a particular point, but it can be either point that correspond to 1 or 2. Let's have (0,8) be the 1 subscripts and (6,-4) be the 2 subscripts:

`(-4-8)/(6-0)=(-12)/(6)=-2`

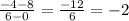
So now we know that the slope is -2. Let's plug this into the equation for m, and use the point (0,8) to solve for b, the y-intercept:

`8=-2(0)+b`

`b=8`

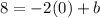
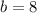
So then we can plug b into the equation and we have the slope-intercept form of the equation:

`y=-2x+8`