I only see the polynomial
 , so I'll factor that one.
, so I'll factor that one.
We can use two approaches: the most "standard" one requires us to find the roots of the polynomial. Then, for each root
 we write the factor
we write the factor
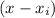 , and decompose the polynomials like this:
, and decompose the polynomials like this:
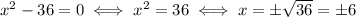
So, the root
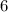 yields the factor
yields the factor
 , and the root
, and the root
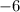 yields the factor
yields the factor
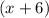 . This means that the polynomial can be factored as
. This means that the polynomial can be factored as
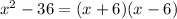
Alternatively, you can observe that the polynomial comes in the form
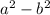 , and it can be factored as
, and it can be factored as
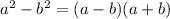
which again leads to
