Question

One runner passes another runner traveling in the same direction on a hiking trail. the faster runner is jogging 4 miles per hour faster than the slower runner. determine how long it will be before the faster runner is five eighths mile ahead of the slower runner.

Answer 1

Both runners are running at a constant speed. Say that the fastest runner goes at speed
`v_f` (for fast) and the slowest goes at speed
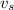`v_s` (for slow).

Let's start the observation at the moment of the passing: the two runners are in the exact same position. The laws that determine their position in the future are

`\text{fast runner: } s_f = v_ft,\quad \text{slow runner: } s_s = v_st`

This means that the difference between the two positions is given by

`s_f-s_s = v_ft-v_st = (v_f-v_s)t`

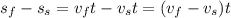
Now we plug in the fact that the faster speed is four more than the slower speed, i.e.
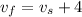`v_f = v_s+4`. The equation for the difference becomes

`s_f-s_s = (v_f-v_s)t = (v_s+4-v_s)t = 4t`

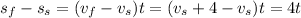
And we want this difference to be 5/8 miles, so the request is

`\cfrac{5}{8} = 4t`

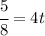
To solve for t, divide both sides by 4 to get

`\cfrac{5}{32} = t`

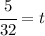
So, after 5/32 of a hour the two runners will be at 5/8 miles from each other.