Question

Solve the simultaneous equation y-2x+1=0 and 4x^2+3y^2-2xy=7

Answer 1

The first equation is
`y-2x+1=0`

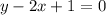
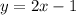`y=2x-1` (Equation 1)

The second equation is
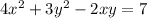`4x^(2)+3y^(2)-2xy=7` (Equation 2)

Putting the value of x from equation 1 in equation 2.

we get,

`4x^(2)+3(2x-1)^(2)-2x(2x-1)=7`

`4x^(2)+3(4x^(2)+1-4x)-4x^(2)+2x=7`

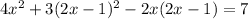
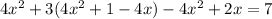
by simplifying the given equation,

`12x^(2)-10x-4=0`

`6x^(2)-5x-2=0`

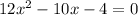
Using discriminant formula,

`D=b^(2)-4ac`

`D=25-4 * 6 * -2 = 73`

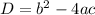
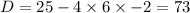
Now the formula for solution 'x' of quadratic equation is given by:

`x=(-b+√(D))/(2a) and x=(-b-√(D))/(2a)`

`x=(5+√(73))/(12) and x=(5-√(73))/(12)`

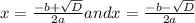
Hence, these are the required solutions.