Vapor pressure of the solution = Partial pressure of ethanol + partial pressure of water.
Partial pressure of ethanol can be calculated from the molefraction of ethanol and vapor pressure of pure ethanol at
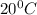
Density of ethanol = 0.800 g/mL
Finding out mass of ethanol =

Moles of ethanol =
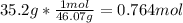
Density of water = 1.00 g/mL
Mass of water =
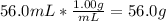
Moles of water =
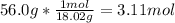
Total number of moles of the solution = 0.764 mol + 3.11 mol = 3.874 mol
Molefraction of ethanol =
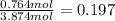
Molefraction of water =
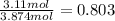
Vapor pressure of pure ethanol at
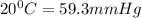
Vapor pressure of pure water at
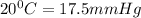
Using Raoult's law to find out partial pressures:
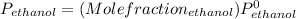
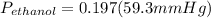 = 11.68 mmHg
= 11.68 mmHg
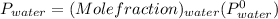
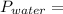
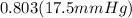 = 14.05 mmHg
= 14.05 mmHg
Total vapor pressure of the solution = 11.68 mmHg + 14.05 mmHg
= 25.73 mmHg