The given sequence is 4,12,36,108....
Here we can observe the first term
 = 4 ,
= 4 ,
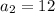 and so on.
and so on.
The common ratio (r)=
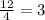
Since the common ratio is greater than 1,
Therefore the sum of the geometric series =
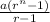
Since we have to find the sum of first seven terms, so n=7
=
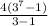
=4372.
Therefore, option C is the correct answer.