The mass of the black hole is

The proton moves in a circular orbit of radius r around the black hole with a speed v. The centripetal force required by the proton is provided by the gravitational attractive force between the proton and the black hole.
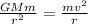
Here, the mass of the black hole is M, the mass of the proton is m and G is the universal gravitational constant.
Rewrite the expression for M.

Substitute
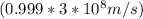 for v,
for v,
 for r and
for r and
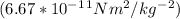 for G.
for G.
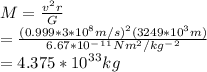
Therefore, the best option from the given values is
