Answer:
a)
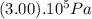
b)
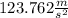
Step-by-step explanation:
Let's start defining the following unit of pressure :

Where N is newton and m is meter.
Within a mass of liquid and defining the surface of the liquid as depth 0.00 m, we can calculate the absolute pressure in any point of the liquid as :
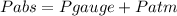
Where Pgauge is the pressure because of the height of liquid over the point.
Where Patm is the atmospheric pressure.
The gauge pressure in a point of a mass of liquid is define as :
Pgauge = δ.g.h
Where δ is the density of the liquid.
Where g is the acceleration due to gravity.
Where h is the height of liquid over the point.
Using the data from the exercise :
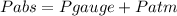
At a depth of 2.00 m :
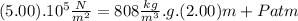 (I)
(I)
At a depth of 5.00 m :
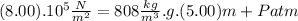 (II)
(II)
In (II) :
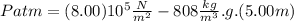 (III)
(III)
Putting (III) in (I) :
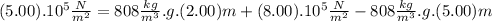
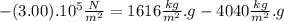
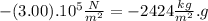
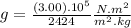
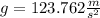
This is the gravity for point b)
For a) we need to replace this value in another equation. For example in equation (III) :


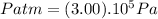
And that is the value of atmospheric pressure on planet x.