Question

Please someone answer

Answer 1

Here triangles CMX and CDS are similar. SO we use the ratio rule of similar triangles which states that the ratio of the corresponding sides are in same proportion . That is

`(SM)/(XD)=(CS)/(CX)`

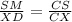
Let SX=x

`(7)/(9) = (15)/(15+x)`

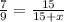
Doing cross multiplication

7(15+x) = 9*15

Distributing 7 on 15 +x ,

105 +7x = 135

Subtracting 105

7x=30

Dividing both sides by 7

x= 4.3

So CX=CS +SX = 15+4.3 = 19.3 or approx 20

Correct option is the first option .