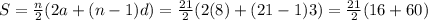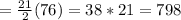Question

Given the Arithmetic series A1+A2+A3+A4 A 1 + A 2 + A 3 + A 4 8 + 11 + 14 + 17 + . . . + 68 What is the value of sum?

Answer 1

Because 17 - 14 = 14 - 11 = 3, the ratio of the arithmetic series is 3;

Then, A4 = 8 - 3 = 5; A3 = 5 - 3 = 2; A2 = 2 - 3 = -1; A1 = -1 - 3 = -4.

But 68 = A1 + ( n- 1 ) x r;

68 = -4 + ( n - 1) x 3;

( n - 1 ) x 3 = 72;

n - 1 = 24;

n = 25;

Finally, Sn = ( A1 + An) x n / 2; then, S25 = ( - 4 + 68) x 25/2;

S25 = 64 x 25 / 2;

S25 = 32 x 25;

S25 = 800;

The value of sum is 800.

Answer 2

Here the first term, a = 8, common difference, d= 11-8= 3 and the last term , l = 68

So before finding the sum, first we need to find the number of terms, and for that we use the formula

a(n) = a+(n-1)d

68 = 8+(n-1)3

Subtracting 8 from both sides

60 = (n-1)3

Dividing both sides by 3

20=n-1

Adding 1 to both sides

n =21

Now we use the formula of sum of n terms of arithmetic series, which is

`S= (n)/(2)(2a+(n-1)d) = (21)/(2)(2(8)+(21-1)3) = (21)/(2)(16+60)`

`= (21)/(2)(76) = 38*21=798`