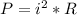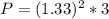Question

A 3.0-ω resistor is connected in parallel with a 6.0-ω resistor. this combination is then connected in series with a 4.0-ω resistor. the resistors are connected across an ideal 12-volt battery. how much power is dissipated in the 3.0-ω resistor? a 3.0-ω resistor is connected in parallel with a 6.0-ω resistor. this combination is then connected in series with a 4.0-ω resistor. the resistors are connected across an ideal 12-volt battery. how much power is dissipated in the 3.0-ω resistor? 12 w 2.7 w 6.0 w 5.3 w

Answer 1

first of all a 3 ohm resistance is connected in parallel with 6 ohm resistance so we will have

`(1)/(R) = (1)/(R_1) + (1)/(R_2)`

`(1)/(R) = (1)/(3) + (1)/(6)`

`R = 2 ohm`

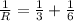
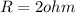
now it is connected in series with 4 ohm resistance

So we will have net resistance given by

`R_(net) = R_1 + R_2`

`R_(net) = 2 + 4 = 6 ohm`

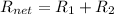
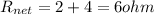
Now this combination of 6 ohm resistance is connected across a battery of 12 V

so now we will have total current in the circuit calculated by ohm's law

`V = i*R`

`12 = i*6`

`i = 2 A`

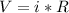
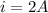
now this 2 A current will divide in 3 ohm and 6 ohm resistance in the ratio of 2:1

so current in 3 ohm resistance is given by

`i = (2)/(2+1)*2= 1.33 A`

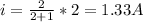
now power dissipated in 3 ohm resistance is given by

`P = i^2 * R`

`P = (1.33)^2* 3`

`P = 5.33 Watt`