Question

What is the approximate area of the unshaded region under the standard normal curve below? Use the portion of the standard normal table given to help answer the questions. See photo’s attached.

Answer 1

its c

Explanation:

Answer 2

Concept:

First find the area of the shaded region under the standard normal curve and after it as you know total area=1 , so 1-area of shaded region= area of unshaded region.

Answer:

Area of shaded region= P(-2
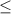`\leq` z
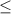`\leq` 1)

Now,

the symbol Ф represent the cumulative density.

first find the

Ф(1) from the above given table it is equal to 0.8413.

Now,

find the Ф(-2) .

in our table we are given the value of Ф(2)=0.9772.

so as the curve is symmetrical Ф(-2)=1-0.9772=0.0228.

P(-2
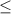`\leq` z
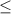`\leq` 1)
= Ф(1)-Ф(-2)

= 0.8413-0.0228

= 0.8185

Now,

Area of unshaded region= 1-area of shaded region

= 1- P(-2
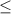`\leq` z
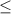`\leq` 1)

= 1- 0.8185

= 0.1815

= 0.18

C is the correct answer.