Question

The position of an object at time t is given by s(t) = -9 - 3t. Find the instantaneous velocity at t = 8 by finding the derivative.

Answer 1

Hello! There are a few ways to find the derivative. One famous formula is below:

Note, t = x = 8

`(f(x + h) - f(x))/(h)`

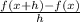
To find the derivative of s(t) = -9 - 3t let insert it into our formula:

`(f(x + h) - f(x))/(h)`

`((-9 - 3(x + h)) - (-9 - 3x))/(h)`

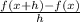
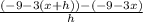
Insert x = 8

`((-9 - 3(8 + h)) - (-9 - 3(8)))/(h)`

Do the Math

`((-9 - 3(8 + h)) - (-9 - 3(8)))/(h)`

`((-9 - 24 - 3h)) + 9 +24))/(h)`

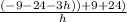
Group Like Terms

`(-9 + 9- 24 +24 - 3h ))/(h)`

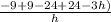
Cancel Terms and Finish Doing The Math

`(-9 + 9- 24 +24 - 3h ))/(h)`

`( -3h )/(h)`

`( -3h )/(h) = -3`

---------------------------------------------------------------------------------------

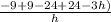
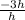
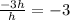
So when t = 8 the instantaneous velocity = -3