We can use a trigonometric function to solve for angle C. We can use any of the trigonometric functions to solve, but today let's use tangent.
Since we know the dimensions of the opposite and adjacent legs, we can solve for theta directly:
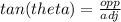
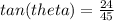
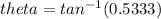
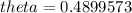 - but this is in radians. So we must convert to degrees.
- but this is in radians. So we must convert to degrees.
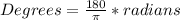
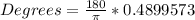
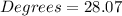
Therefore, the measure of angle C is 28°.