Question

Identify the equation of the circle that has its center at (7, -24) and passes through the origin

Answer 1

To write the equation of a circle we need to know the center and the radius. We are given the center explicitly, and we can deduce the radius: if the circumference passes through the origin, it means that the origin belong to the circumference.

But all points belonging to the circumference have the same distance from the center: the radius! So, the radius of this circumference is the distance between (7, -24) and the origin, which we can compute with the usual formula

`d(A,B) = √((A_x-B_x)^2+(A_y-B_y)^2)`

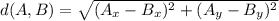
which in this case becomes

`r = d((7, -24),(0,0) = √((7-0)^2+(-24-0)^2) = √(49+576) = √(625) = 25`

Now that we know the center and the radius of the circle, we can write its equation. In general, given the center C = (h,k) and the radius r, the equation is

`(x-h)^2 + (y-k)^2 = r^2`

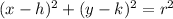
which in this case becomes

`(x-7)^2 + (y+24)^2 = 625`