Question

It is believed that the percentage of people who support candidate A is 56%. A sample of size 100 indicated that 40 people support candidate A. Is there evidence at an alpha level of 10% to conclude that the percentage of people who support candidate A has changed?

Answer 1

Given data:

Sample size
`=100`

Sample proportion of people support candidate A:

`p=(40)/(100)=0.40`

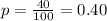
Population proportion of people support Candidate A :

`P=(56)/(100)=0.56`

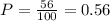
Check the condition:
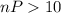`nP>10` and
`n(1-P)>10.`

`nP=100*0.40=40>10`

`n(1-P)=100*0.60=60>10`

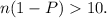
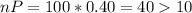
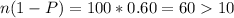
Null Hyposthesis:
`H_0: P=0.56`

Alternative Hypothesis:
`H_\alpha :P\\eq 0.40`

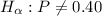
The test statistics:

`z=\frac{p-P}{\sqrt{(P(1-P))/(n)}}`

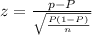
Plug in p=0.56, P=0.40 and n=100 in the above formula,

`z=\frac{0.56-0.40}{\sqrt{(0.40(1-0.40))/(100)}}`

`z=\frac{0.56-0.40}{\sqrt{(0.40(1-0.40))/(100)}}=3.2659`

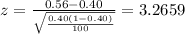
The table value of z at 10% of significance level is 1.28

Table value is less than the calculated value.

Hence
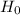`H_0` is rejected at 10% level.

Therefore there is the evidence at an alpha level of 10% to conclude that the percentage of people who support candidate A has changed.