Answer:
The correct answer is the first one.
Explanation:
We have the functions
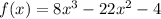 and
and
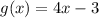 . Then, the fraction is
. Then, the fraction is
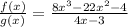 .
.
If we want to give a ‘‘simplified’’ expression for this quotient we must do a a division of polynomials. The algorithm is the analogue for the division of integers. Attached there is an image of the procedure.
After the completion of the division algorithm we obtain
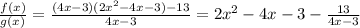 .
.