So first we need to take 2 points. Let's use the first two: (2,9) & (3,12)
We know that the equation to find slope is:
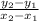
where the subscripts 2 and 1 correspond to either point, the first or the second, either is fine. Let's use (2,9) for the 1 subscripts and (3,12) for the 2 subscripts:
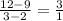
So now we now that the slope of this data set is 3. We can now plug it into the equation:
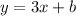
To find the y-intercept for this equation, we need to pick a point and plug it into the equation and solve for b. Let's use (2,9):
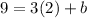
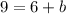
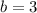
So now we can plug in b and solve for the equation for the data set:
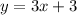
This is the equation that represents the data set that is given and it matches the answer you have circled.