Question

Which is an equation of a circle with center (5, 0) that passes through the point (1, 1)

Answer 1

Equation of circle at center (h,k) is given by

`(x-h)^2+(y-k)^2=r^2`

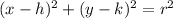
Given that center is at (5,0) that means h=5 and k=0

plug both values into above formula

`(x-5)^2+(y-0)^2=r^2`

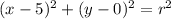
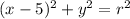`(x-5)^2+y^2=r^2` ...(i)

Given that circle passes through point (1,1) so it will satisfy above equation

`(1-5)^2+1^2=r^2`

`(-4)^2+1^2=r^2`

`16+1=r^2`

`17=r^2`

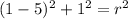
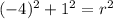
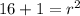
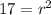
Now plug this value of r^2 into equation (i)

`(x-5)^2+y^2=17`

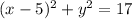
which best matches with choice C

Hence
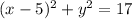`(x-5)^2+y^2=17` is the final answer.