Question

Plz help me I will die if sm one does not answer my question correctly it's the 6th question ....an umbrella ....I have given the picture of the figure just in case u need .plz help I beg of u

Answer 1

10 equal triangles; blue = 5 and grey = 5 (1/2 grey and 1/2 blue)

isosceles triangle has side equal 50 cm and base equal 20 cm

perimeter of triangle = 50 + 50 + 20 = 120 cm

1/2 perimeter (because each color = 1/2) = 120/2 = 60 cm

Area of each triangle = √60(60-50)(60-50)(60-20)

= √(60 x 10 x 10 x 40)

= 10√2400

= 200√6 cm^2

Because blue and grey has 5 triangles

so 200√6 x 5 = 1000√6 cm^2

Answer: Each color needs 1000√6 cm^2 cloth

Answer 2

Let's try to avoid any math fatalities. Yes, the figure is helpful.

In practice this is a difficult problem dependent on the shape of the material from which we're to cut our pieces, and worrying about leftovers. Let's assume in middle school all they're asking for is the area of five blue triangles and the area of five white triangles.

The triangles are isosceles. The bisecting altitude h of an isosceles triangle forms a right triangle with other leg half the base and hypotenuse the common side.

`h^2 + (20/2)^2 = 50^2`

`h^2 = 2500-100=2400`

`h = √(2400) = √(400 * 6) = 20 √(6)`

`\textrm{area of 5 blue triangles} = 5(\frac 1 2 bh)= \frac 5 2 (20)20 √(6)} = 1000 √(6) \approx 2500 \textrm{ sq cm}`

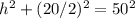
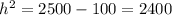
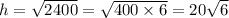
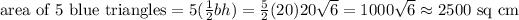
Same amount for the white triangles.

EDIT:

The questioner is the rare student who knows Heron's Formula,

`A = √(s(s-a)(s-b)(s-c)) \textrm{ where } s=(a+b+c)/2`

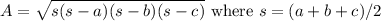
We have the one case which works nicely, integer sides with an even perimeter. s=(50+50+20)/2=60, so

`A = √(60(60-50)(60-50)(60-20)) = √(60(10)(10)(40))=200 \sqrt 6`

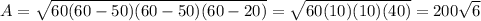
and we need five of those for each color.

There are other formulas, often better than Heron's:

`16A^2 = (a+b+c)(-a+b+c)(a-b+c)(a+b-c)=4a^2b^2-(c^2-a^2-b^2)^2=(a^2+b^2+c^2)^2 - 2(a^4+b^4+c^4)`

I'll leave those for you to derive for yourself; start from Heron.