The side of an equilateral triangle inscribed in a circle is √3*r. So,
l=√3*r Where l= side of equilateral triangle and r= radius of circle.
Given the side length: l= 12√3. So, plug in l=12√3 in the above formula.
12√3= √3*r
So, r= 3 (Dividing each sides by √3).
So, the radius of the circle is 3 units long.
Formula to find the apothem is:
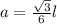
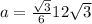
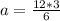 Since√3*√3= 3
Since√3*√3= 3
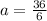
a=6
So, apothem is 6 units long.