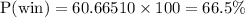Answer: C. 66.5%
Explanation:
Given: Arnold is playing a game where he is trying to roll a two with a standard die.
We know that for any event P(A) = 1 - P(A')
Therefore, P(win)=1-P(lose)
Thus, he loses if he never rolls a 2 in the 6 rolls.
The total number of outcomes = 6
There number of losing outcomes (1, 3, 4, 5, 6)=5
Therefore, the probability that Arnold loses the game is given by :-
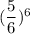
Now, the probability that Arnold wins the game is given by :-
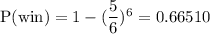
In percent, the probability that Arnold wins the game is given by :-