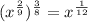Question

Simplify open parentheses x to the 2 ninths power close parentheses to the 3 eighths power.

x to the 5 seventeenths power
x to the 1 twelfth power
x to the 11 over 72 power
x to the 43 over 72 power

Answer 1

Option 2

`(x^{(2)/(9)})^{(3)/(8)}=x^{(1)/(12)}`

Explanation:

Given : Open parentheses x to the 2 ninths power close parentheses to the 3 eighths power.

To find : Simplify the given expression?

Solution :

Open parentheses x to the 2 ninths power close parentheses to the 3 eighths power i.e,
`(x^{(2)/(9)})^{(3)/(8)}`

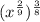
Applying the power rule of exponent,
`(x^a)^b=x^(a\cdot b)`

`(x^{(2)/(9)})^{(3)/(8)}`

`=x^{(2)/(9)*(3)/(8)}`

`=x^{(2* 3)/(9* 8)}`

`=x^{(6)/(72)}`

`=x^{(1)/(12)}`

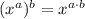
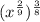
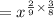
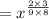
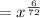
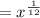
Therefore, Option 2 is correct.

`(x^{(2)/(9)})^{(3)/(8)}=x^{(1)/(12)}`

Answer 2

The given expression is

`(x^(2/9))^(3/8)`

Here we have two exponents, so we have to use power of a power rule of exponent , in which we need to multiply the exponents . And on doint this, we will get

`x^({2/9}*{3/8}) =x^(6/72) = x^(1/12)`

And it is equal to x to the 1 twelfth power. SO the correct option is the second option .