Question

A(4,-1) B(0,7) C(2,m) This is a triangle center of gravity of the triangle on the x-axis what is the triangle area. emergency emergency emergency

Answer 1

The center of gravity of a triangle is also known as the centroid, the meet of the medians, the segments from the midpoint of a side to the opposite vertex.

The centroid is easily calculated from the average of the coordinates. We know the centroid is on the x axis, i.e. the y coordinate is 0. That's the equation:

`0 = \frac 1 3 ( -1 + 7 + m)`

`m = -6`

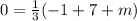
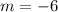
Now we have the three vertices of a triangle. We can calculate the area with the shoelace formula:

(4,-1),(0,7),(2,-6)

(0,7),(2,-6),(4,-1)

`\textrm{area} = \frac 1 2 |4(7) - -1(0) + 0(-6)-7(2) + 2(-1)- -6(4) | = \frac 1 2 |36|=18`

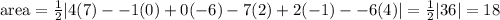
Answer: 18