The given radical expression is
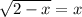
Squaring on both the sides of the equation, we get
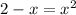
Bringing all the variables and constant to the right side of the expression, so we get:
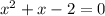
By comparing the above expression with the standard form

we get a=1, b=1 and c= -2
Discrimant(D) =
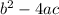
Discrimant(D)=
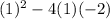
D=9
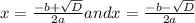
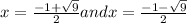
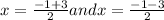
x= -1 and 2 are the required solutions of the given radical expression.