Question

A worker is paid $0.10 on the first day, $0.30 on the second day, $0.90 on the third day, $2.70 on the fourth day, and so on. How much money (rounded to the nearest cent) in total does the worker earn after working 14 days

Answer 1

A worker is paid $0.10 on the first day, $0.30 on the second day, $0.90 on the third day, $2.70 on the fourth day, and so on.

Notice that the pattern of getting wages is 3 times of the previous day.

Like the wages for the first day= 0.10

Second day = 0.10*3 = 0.30

Third day = 0.30 *3 = 0.90 And so on.

Hence the wages represent a geometric sequence where

first term: a = 0.10 and common ratio: r = 3.

And we need to find the total does the worker earn after working 14 days:
`S_(14)`.

Formula to find the sum of nth term a geometric sequence is:

`S_(n) =(a(r^n-1))/(r-1)`

=
`(0.10(3^(14)-1))/(3-1)`

=
`(0.10(4782969-1))/(2)`

=
`(0.10(4782968))/(2)`

=
`(478296.8)/(2)`

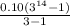
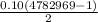
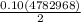
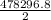
= 239148.4

So, he will earn $239148.40 fter 14 days.

Hope this helps you.