Question

Circles M and K are congruent, QR is congrent to LN. Find the length of QR

Answer 1

Given QR is congrent to LN and QR = 4x + 2 and LN = x + 7.

So, QR = LN

Hence, we can set up an equation as following:

4x + 2 = x + 7

4x + 2 - x = x + 7 - x Subtract x from each sides.

3x + 2 = 7 By simplifying.

3x + 2 - 2 = 7 - 2 Subtract 2 from each sides.

3x = 5

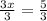`(3x)/(3) =(5)/(3)` Divide each sides by 3 to isolate x.

So,
`x=(5)/(3)`

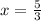
Next step is to plug in
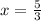`x=(5)/(3)` in QR = 4x+2 to get length of QR.

So,
`QR = 4((5)/(3))+2`

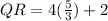
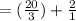`=((20)/(3))+(2)/(1)` Since 2 can be written as 2/1.

By multiplying the second fraction by the common denominator 3.

`=((20)/(3))+(2*3)/(1*3)`

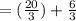`=((20)/(3))+(6)/(3)` By simplifying the second fraction.

`=((26)/(3))`

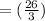
So,
`QR=(26)/(3)`