Question

Please show how f(x)=(2x+3)/(x-2) is continue in the interval ]2,infinity[

Answer 1

See below

Explanation:

A function is continuous within an interval if its first derivative exists

`\text{The first derivative of }(2x+3)/(x\:-\:2) = (d)/(dx)\left((2x+3)/(x\:-\:2)\right) = -(7)/(\left(x-2\right)^2)`

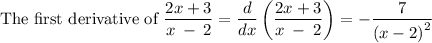
Let's call this first derivative g(x)

g(x) is defined at all values of x except at x=2 since at this value the denominator becomes 0 and g(x) is not defined.

So the function has a discontinuity at x = 2

But in the interval (2, ∞ ) the function g(x) always has a real value so f(x) is continuous in that interval