Question

The u. s. treasury issued a 10-year bond on november 16, 1998, paying 6.47% interest. thus, if you bought $600,000 worth of these bonds, you would receive $38,820 per year in interest for 10 years. at investor wishes to buy the rights to receive the interest on $600,000 worth of these bonds. the amount the investor is willing to pay is the present value of the interest payments, assuming a 6% rate of return. if we assume (incorrectly, but approximately) that the interest payments are made continuously, what will the investor pay?

Answer 1

The investor will pay $ 21,304.88 to receive an annuity of $38,820 each year for 10 years at 6% interest compounded continuously.

Given :

Interest on $600,000 worth of bonds = $38,820 per year

No. of years = 10 years

Discount rate = 6%

Compounding interval = Continuous compounding ( as given in the question)

We use the following formula to arrive at the Present Value:

`PV = C /e^(rt)`

`PV = 38820 /2.71828^(0.06*10)`

`PV = 38820 /1.822118065`

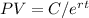
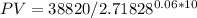
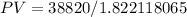
PV = $ 21,304.88