So we are given an initial equation of:
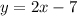 .
.
We are told that a new path is going to be perpendicular to this line. So to find a slope that is perpendicular to a line, we take the slope of the known line (in this case 2) and we flip it and change the sign. So since this slope is essentially
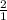 , we are going to flip it to make it
, we are going to flip it to make it
 and change the sign to make it
and change the sign to make it
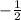 .
.
So now we know that the slope of the perpendicular line is
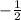 , we can start a new equation for this line:
, we can start a new equation for this line:
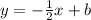
We are also told that the path will intersect at (-2,-3) - this is a solution to the two lines. So to find b in this new equation, let's plug in the x and y values found in the point:
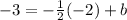
Then solve for b:
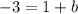
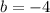
So then we plug in our value for b and leave x and y:
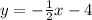
So this equation now represents the new path.