The formula for conditional probability is as following:
P(A/B')=P(A∩B') /P(B')
Given P(A ∩ B')=
 and P(B')=
and P(B')=
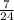 .
.
So, first step is to plug in the given values in the above formula to get the answer. Hence,
P(A/B')=
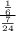
=

(Multiplying both top and bottom by 24).
=

So, P(A/B')=

Hence, the correct choice is B:
