Question

Can anyone help me out?

Answer 1

I'm going to take a stab at this hoping that I get it right! Looking at your graph, you see a hole at x = 3. That means that that is a removable discontinuity. This results from the factor (x-3) canceling out between the numerator and the denominator of the rational function. The other discontinuity is found at the vertical asymptote at x = -4, which in factorization form is (x+4). That means that the 2 factors in the denominator are (x-3) and (x+4). If you factor the numerator you see that the factors are (x-3)(x-1), hence the reason that there is a hole in the graph at x = 3. If you FOIL out (x-3)(x+4) you get

`x^2+x-12`

so a = 1 and b = -12. Again, I THINK that's correct...

Answer 2

we are given

`f(x)=(x^2-4x+3)/(x^2+ax+b)`

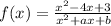
we need to find a and b

we can see that there is a hole at x=3

It means that (x-3) will be factor in both numerator and denominator

so, if we plug x=3 in the denominator we will get denominator value as 0

`(3)^2+3a+b=0`

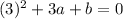
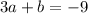`3a+b=-9`.........(1)

we can see that

there is a vertical asymptote at x=-4

so, denominator must be zero at x=-4

`(-4)^2-4a+b=0`

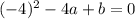
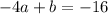`-4a+b=-16`.........(2)

we can subtract equation-1 and equation-2

we will get

`a=1`

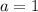
now, we can find b

`3*1+b=-9`

`b=-12`

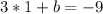
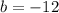
so, we will get

`a=1`

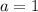
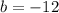`b=-12`..............Answer