Question

Mother gives birth to a 8 pound baby. Every 4 months, the baby gains 3 pounds.

If x is the age of the baby in months, then y is the weight of the baby in pounds.

Find an equation of a line in the form y = mx + b that describes the baby's weight.

Answer 1

Hello!

The equation, y = mx + b is slope-intercept form. In this equation, m is the slope, and b is the y-intercept.

If the baby was exactly 8 pounds when it was born, then the y-intercept is (0, 8) because at zero months, the baby was eight pounds. To find the rate of change, we can use the the y-intercept (0, 8), and the weight of the baby at four months, which is (4, 8 + 3) → (4, 11).

Since we have two points, we can use the slope formula
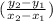`((y_(2)-y_(1))/(x_(2)-x_(1)))` to find the rate of change.

`(8 -11)/(0-4) = (-3)/(-4) = (3)/(4)`.

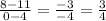The rate of change is 3/4.

Therefore, the equation that describes the baby's weight is y = 3/4x + 8.