Question

A car travels at 8,800 feet per minute. If the radius of the tire on the car is 2 feet, how many revolutions does one of these tires make in three minutes?(22/7=pi)

Answer 1

A revolution is once around the outside measure of the tire. This is also known as the circumference of a circle. The circumference of this tire is found in the formula

`C=2\pi r`

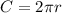
where r is the radius of the tire and pi is given as the fraction equivalent 22/7. If we fill in the formula accordingly, we have

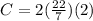`C=2((22)/(7))(2)` and the circumference is
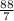`(88)/(7)`. This means for us that the tire travels a total of 88/7 feet in 1 revolution. If the tire travels 8,800 feet in one minute, we need to find out how moany revolutions this is equal to. We find this out by dividing 8,800 by 88/7. Doing this looks like this:

`(8800)/(1)*(7)/(88)`.

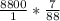Remember that when we divide fractions, we bring up the bottom fraction and flip it to multiply. That means that the tire makes 700 revolutions in 1 minute. In 3 minutes it makes 700 times 3 which is 2100 revolutions.