Question

Consider the function
`f(x)=-x^2+27x-9`. The slope of the tangent line to f(x) at
`x=-9` is ___ . The value of f(x) at
`x=-9` is ___ . The y-intercept of the tangent line at
`x=-9` is ___ .

Answer 1

Explanation:

Answer 2

`f(x)=-x^2+27x-9`

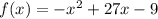
We know that first derivative gives the slope of the given equation.

First derivative of the given function is given by formula d/dx(x^n)=nx^(n-1)

so first derivative will be

`f'(x)=-2x^1+27(1x^0)-9(0)`

`f'(x)=-2x+27`

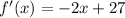
now to find the slope at x=-9, plug it into above equation

`slope = f'(-9)=-2(-9)+27 =18+27 =45`

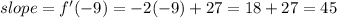
Hence slope of tangent at x=-9 is 45.

----------------

To find the value of f(x) at x=-9 we just plug x=-9 into given equation.

`f(x)=-x^2+27x-9`

`f(-9)=-(-9)^2+27(-9)-9`

`f(-9)=-81-243-9`

`f(-9)=-333`

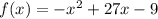
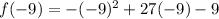
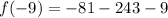
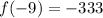
Hence value of f(x) at x=-9 is f(-9)=-333.

----------------------------

To find y-intercept of the tangent line, first we need to find the equation of tangent line.

at x=-9, we got f(x)=-333 so that means tangent line passes through point (-9,-333)

we also know slope of tangent is m=45

now plug those values into formula y=mx+b

-333=45(-9)+b

-333=-405+b

-333+405=b

72=b

In y=mx+b, b shows y-intercept.

Hence required y-intercept of the tangent line at x=-9 is 72.