Let's try to simplify that a bit. Rewriting it in its current form it looks like this:
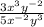 .
.
We could split it up and deal with one problem at a time if we do this:
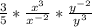 .
.
The rule with like bases and division of the exponents is that we subtract the lower exponent from the upper so that would be
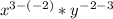
which gives us new exponents of
 .
.
We rewrite to make that negative exponent a positive by putting it under a 1, so the whole problem with no negatives looks like this now:
 .
.
If x = 2 and y = 3, we sub in accordingly:
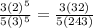
which simplifies to
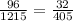 , the first choice above.
, the first choice above.