We know that angle subtended at the center of the circle is always double of the angle subtended at the perimeter of the circle created from same points.
So according to attached picture,
m∠B=2*(m∠D)
or m∠B=2*(65)
or m∠B=130
Now we know the central angle B = 130 degree which is subtended by arc length "x"
so we can use arc lenght formula to find the value of x
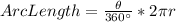
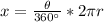
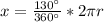
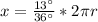

Since value of radius of the circle is not given so we will stop here
Hence final answer is
