Question

A. identify the parent function of the given graph.

B. in TWO OR MORE COMPLETE SENTENCES, compare and contrast the domain and range of the parent function with the that of the given graph.

Answer 1

The parent function is f(x) = x^3

The domain are all x values (-infinity, infinity)

The range are all y values (-infinity, infinity)

Answer 2

The parent function for the provided graph is
`y=x^3`.

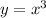Domain of the provided function is
`(-\infty,\infty)`.

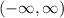Range of the provided function is
`(-\infty,\infty)`.

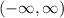Explanation:

Consider the provided information.

Vertical Transformations:

The graph of parent function f(x) move up b unit for f(x)+b.

The graph of parent function f(x) move down b unit for f(x)-b.

Part (a)

Here, we need to identify the parent function of the given graph:

The graph of the provided function is same as the graph of
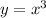`y=x^3` shifted vertically down by 2 unit.

The graph of
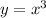`y=x^3` is shown in figure 1:

Thus, the parent function of given graph is
`y=x^3`.

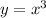Part (b)

The domain is the set of input values which a function can take, or the domain is the set of all possible x values.

Range is the set of y values or the values produced by the function.

The range and domain of the parent function is all real number.

Now consider the provided function.

The provided function is defined for any value of x. Thus, the domain of the function is:
`(-\infty,\infty)`

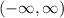
The range of the function is the set of y values and the set of y values is all real number, Thus the range of the provided function is
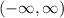`(-\infty,\infty)`.