Question

Triangles MOP and MNQ are similar. Find x.

Answer 1

Aight so if you add the angel mn and no you get eight so that must mean the opposite side must also equal eight, in that case 8-4 is 4, so Qp is 4

correct me if im wrong

Answer 2

The value of x is 4/3.

Explanation:

It is given that triangles MOP and MNQ are similar.

The corresponding sides of similar triangles are proportional.

`(MQ)/(MP)=(MN)/(MO)`

`(MQ)/(MQ+QP)=(MN)/(MN+NO)`

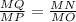
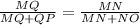
It is given that MQ=4, QP=x, MN=6, NO=2. Put this value in the above equation.

`(4)/(4+x)=(6)/(6+2)`

`(4)/(4+x)=(6)/(8)`

`4* 8=6(4+x)`

`32=24+6x`

`32-24=6x`

`8=6x`

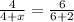
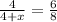
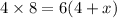
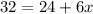
Divide both sides by 6.

`(8)/(6)=x`

`(4)/(3)=x`

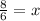
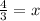
Therefore the value of x is 4/3.