Question

Point C is the center of the circle. If angle ACB measures (1/2x + 6) degrees and arc AB measures (x + 1) degrees, find x

Answer 1

If point C is the center of the circle, the angle ACB is a central angle. A central angle and the arc it intercepts have the same measure in degrees. So if they are the same, we will set them equal to each other in an equation to solve for x.

`(1)/(2)x+6=x+1`.

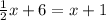We will subtract 1 from both sides, and at the same time subtract 1/2x from both sides to get

`(1)/(2)x=5`.

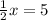We need to solve for x so that means getting rid of the fraction. We will do that by multiplying both sides by 2 to get x = 10. That's your answer!

Answer 2

From the facts about a circle, we know that the angle (angle ACB in the diagram) subtended by an arc (arc AB in the diagram) of a circle on its center (point C in the diagram) is always equal to measure of the same arc AB.

It means arc AB = angle ACB

`x + 1 = (1)/(2) x + 6 \\ x - (1)/(2)x \: = \: 6 - 1 \\ (1)/(2)x \: = 5 \\ x = 5 * 2 = 10`
Hence, x = 10 is the final answer.