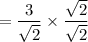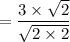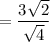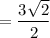Question

How do you rationalise the denominator

Answer 1

Before we figure out how to rationalize a denominator, we must first understand what rationalizing a denominator does. You can rationalize a denominator when there is an irrational number (like a square root) in the denominator. To rationalize the denominator, we want to get rid of the square root/irrational number in the denominator. We can do this by multiplying by the conjugate of the denominator. The conjugate of a complex number (a number that has an irrational part) is the opposite of that number (a number that would have the opposite parity). Now, to rationalize the denominator, we multiply the fraction by the conjugate of the denominator over the conjugate of the denominator (which is equal to one). This always rationalizes the denominator.

Answer 2

You must multiply the numerator and denominator by a specific root that makes the denominator become a perfect root and rational.

Here is an example. Rationalize the following denominator:

`(3)/(√(2)) =`

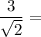
By multiplying sqrt(2) by sqrt(2), you get 2 which is rational. Therefore, multiplying the denominator by sqrt(2) will accomplish the goal of rationalizing the denominator. Of course, since we a dealing with a fraction, we must multiply both the numerator and denominator by the same number to generate an equivalent fraction, so we multiply both the numerator and denominator by sqrt(2). Then we simplify and reduce the fraction.

`= (3)/(√(2)) * (√(2))/(√(2))`

`= (3 * √(2))/(√(2 * 2))`

`= (3√(2))/(√(4))`

`= (3√(2))/(2)`