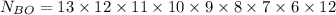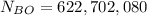The total number of permutations is the product of the number of options for each choice:
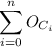
For the first position there are 13 choices, for the second 12 and so on. This pattern holds until the last spot which we are told must be one of the 12 pitchers. Thus: