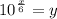ANSWER
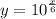
Step-by-step explanation
The logarithmic equation given to us is
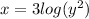
Recall this property of logarithms,
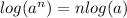
We apply this property to the right hand side to obtain,
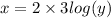
This implies that,

We now divide both sides by 6 to get,
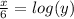
We now take antilogarithm to get,