Answer:
The required number in teh polynomial needs to be changes to make it a perfect cube is
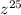 .
.
Explanation:
Given : Expression
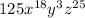
To find : Which number in the monomial expression needs to be changed to make it a perfect cube?
Solution :
Expression
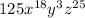
Using property,
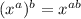 and
and

Now we distribute each term into a power cube.
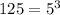
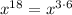
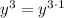
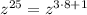
We have seen that
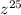 is not making a multiple of 3 so to make it a perfect cube we have to change it into
is not making a multiple of 3 so to make it a perfect cube we have to change it into

Now, Making a perfect cube with the change
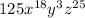
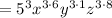

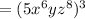
Therefore, The required number in teh polynomial needs to be changes to make it a perfect cube is
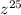 .
.